DIP:  Black and white image morphology

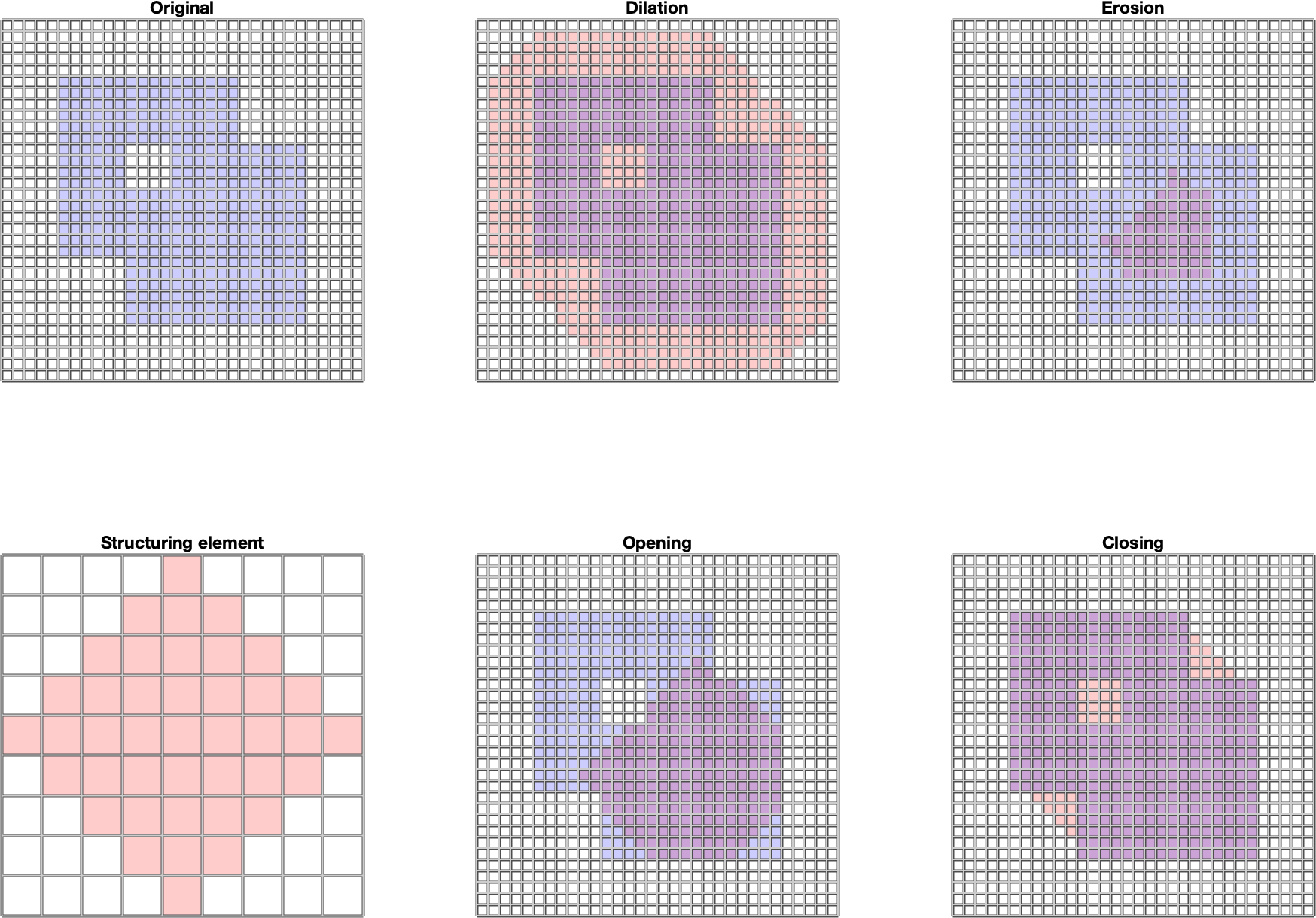
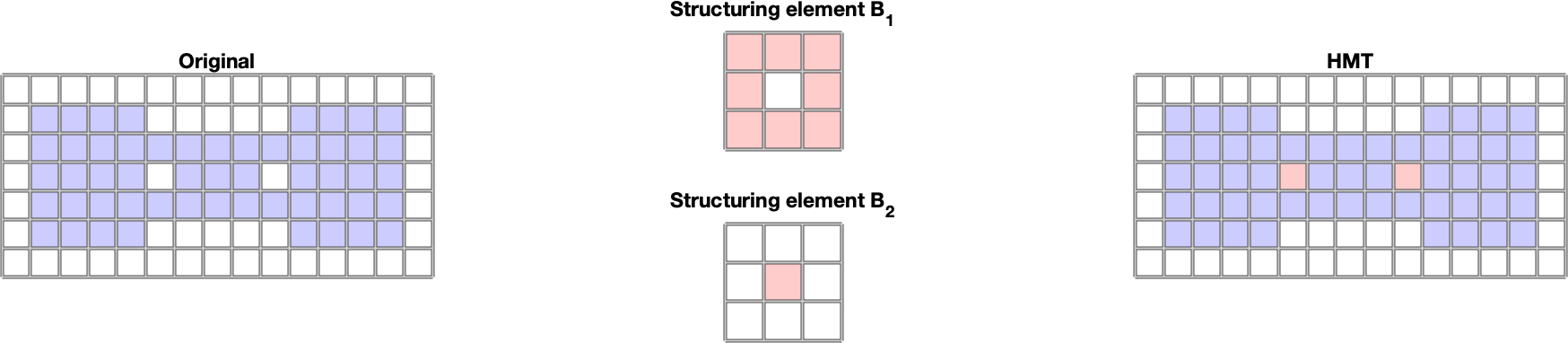
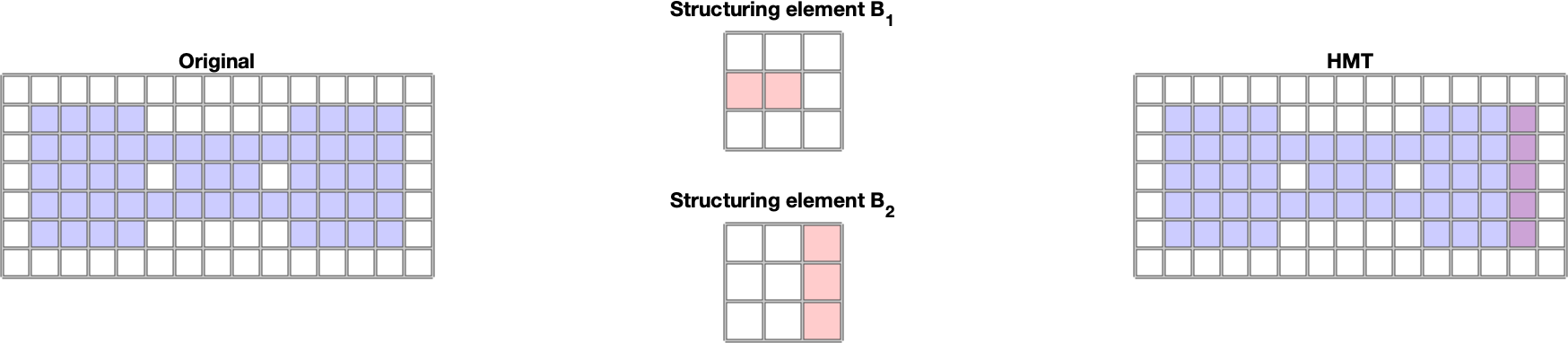
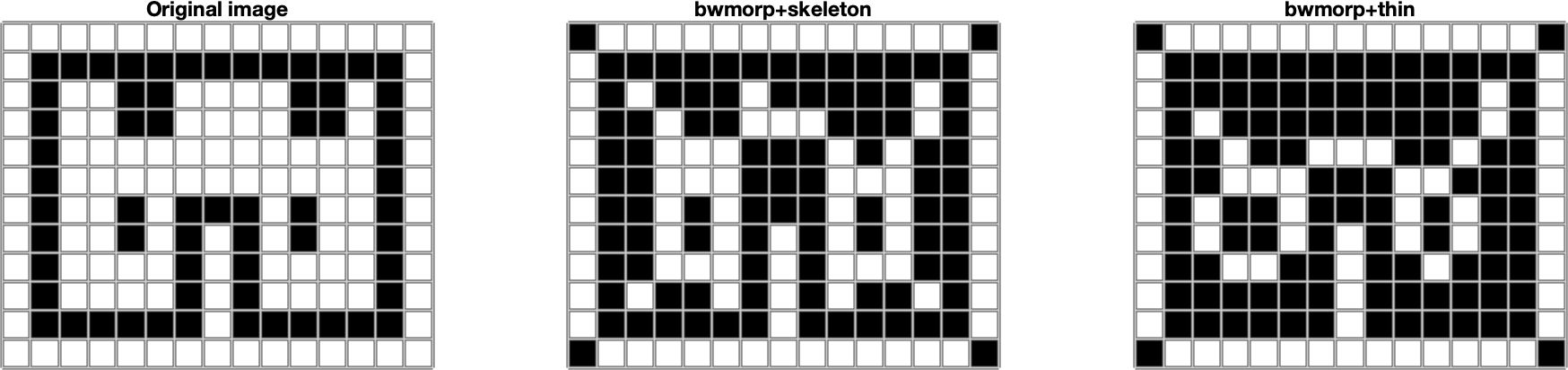
In this section, we present the basic definitions and operations of morphology with a black and white (i.e. binary) image. Let \(E\) be the Euclidean space \(Z^2\). I.e. it is the space of all pairs of integer numbers. Let \(B\) be the set of points from \(E\), e.g.: \(B\)={(-1,0), (0,-1), (0,0), (0,1 ), (1,0)}. Then translating the set \(B\) by the vector \(z\) we call the set \(B_z\) for which:

\[B_z=\{b+z | b \in B\}, \forall z \in E\]

By mirroring the set \(B\) we denote the set \(\hat{B}\), while the following applies:

\[\hat{B}=\{x \in E | -x \in B\}\]

Let \(A\) be a black and white image - a set of points \(A\) in the space \(E\) to which we assign a rectangular border. By structural element we will understand such a set \(B\) to which we assign center at the point \(0,0\). Then by erosion of the image \(A\) using the structural element \(B\) we call the set:

\[A\ominus B=\{z \in E | B_z \subseteq A\}\}\]

I.e. is the set of points where the center of \(B\) goes when the set \(B\) moves within the set \(A\).

By dilating the image \(A\) using the structural element \(B\), we call the set:

\[A\oplus B=\{z \in E | \{\hat{B}_z \cap A \neq \emptyset\}\}\]

T.. is the set of points where the center of \(B\) reaches when the set \(B\) moves so that it still overlaps at least partially with \(A\).

Opening the image \(A\) using the structural element \(B\) is the set:

\[ A \circ B = ( A \ominus B) \oplus B\]

I.e. it is the set of points covered by \(B\) points when the set \(B\) moves within the set \(A\)..

Closing the image \(A\) using the structural element \(B\) is the set:

\[ A \bullet B = ( A \oplus B) \ominus B\]

I.e. it is the set of points not covered by \(B\) points when the set \(B\) moves so that it does not overlap with \(A\).

Erosion and dilation as well as opening and closing are complementary operations. Let \(^C\) denote the complementary set. Then applies:

\[(A\ominus B)^C = A^C \oplus \hat{B}\]

\[(A\oplus B)^C = A^C \ominus \hat{B}\]

\[(A\circ B)^C = A^C \bullet \hat{B}\]

\[(A\bullet B)^C = A^C \circ \hat{B}\]

In the MATLAB environment, they are implemented using the functions imerode, imdilate, imopen, imclose. The structural element is created using the strel function and is a rectangular area. The complementary image can be obtained using the imcomplement function. More information can be found in [1]. Examples of the mentioned basic morphological operations for a black and white image are shown in Fig. 1.

Fig. 1 Examples of basic morphological operations for a black and white images: erosion, dilation, opening, closing . For clarity, the original image, the structural element and the result of the morphological operations are color-differentiated using the red and blue color channels, and blending using the alpha channel is used.

Basic morphological operators allow to detect object boundaries using the operation:

\[A-A\ominus B\]

I.e. we subtract the eroded image from the original image, so we are left with an edge. Examples of use are shown in Fig. 2

A more advanced morphological operation used in shape recognition is the hit or miss transformation (HMT). This operation works with two structural elements \(B_1, B_2\). The result is the set:

\[A \circledast B_{1,2}=(A\ominus B_1)\cap(A^C \ominus B_2) \]

This operation allows to interpret points absent in the image and structural element as background. If we choose \(B_2=B_1^C\), i.e. \(B_2\) represents the background and interpret \(A\) with \(A^C\) as foreground and background, then the HMT results are the positions of the center of the structural element \(B_1\) where its foreground is in the foreground \( A\) and at the same time its background is in the background \(A\). In the MATLAB environment, the HMT is available using the bwhitmiss function. An example of HMT is shown in Fig. 3. HMT allows us to define, in addition to the foreground and background, which points we do not care about. These are the ones that do not appear in either \(B_1\) or \(B_2\). An example of the use of such structural elements is Fig. 4.

Morphological reconstruction is an iterative method for area reconstruction, which uses 2 images and a structural element. The first image (marker - \(F\)) determines the starting point (points), the second determines the target area (mask - \(G\)). The structural element \(B\) determines the connectivity. The reconstruction is denoted by \(R_G^F\) and is calculated as follows:

Initialize \(h_1=F\)
Repeat \(h_{k+1}=(h_k\oplus B) \cap G\) until \(h_{k+1}=h_k\)
The output is \(R_G^F=h_{k}\)

If there are several objects in the image, they can be separated using morphological reconstruction (each marker identifies a different object). Alternatively, empty bounded areas can be filled with this algorithm (if \(A\) is an area, then we choose \(A^C\) as a mask). In the MATLAB environment, reconstruction is available using the imreconstruct function. Examples of both uses are in Fig. 5 and 6. Morphological reconstruction is also used by the function imfill.

When processing the image, it can be useful to get a skeleton of the specified area. The skeleton is a set of connected points that are equidistant from the edge of the area. Morphologically, this set can be obtained by repeated thinning of the area, e.g. using erosion, while preserving endpoints and line connectivity (we also talk about topologically preserving thinning). In the MATLAB environment, this operation is available using the bwmorph function, while "thin" or "skel" (algorithm described in [4]) is selected as the operation. "glass" (uses algorithm [4]). Operations give a slightly different result. An example is shown in Fig. 7.

Fig. 2 An example of object boundary detection using morphological operations for a black and white image. For clarity, the original image, the structural element and the result of the morphological operation are color-differentiated using the red and blue color channels, and blending using the alpha channel is used.

Fig. 3 Example of detecting holes in an object using HMT.

ig. 4 Example of detecting the right edge of an object using HMT..

Fig. 5 Example of morphological reconstruction of part of the object based on the initial markup.

Fig. 6 Example of morphological reconstruction used to fill the object.

Fig. 7 An example of creating a skeleton of an area using morphology in the MATLAB environment.

More information about morphological operations can be found in [2] [3].

References

[1] Mathworks, Morphological Operations, online: \url{https://www.mathworks.com/help/images/morphological-filtering.html}

[2] Gonzalez, R., C., Woods, E., W., Digital Image Processing, Global Edition, 4th edition, Pearson 2018, ISBN 10: 1-292-22304-9

[3] Gonzalez, R., C., Woods, E., W., Eddings, S., L., Digital Image Processing using MATLAB, Gatesmark Publishing, ISBN-10: 0-9820854-1-9

[4] Haralick, Robert M., and Linda G. Shapiro. Computer and Robot Vision, Volume I. Addison-Wesley, 1992.

Appendix

The source code of the program that created Fig. 1

%https://en.wikipedia.org/wiki/Alpha_compositing
% RGBA images have 4 layers, the 4th is alpha channel:
% alpha value of 0 means that the pixel is fully transparent 
% alpha value of 1 means that the pixel is fully opaque.
clear all; close all; clc;
fig=figure;
%create some demo images
A=zeros(32,32);
A(6:21,6:21)=ones(16);
A(12:27,12:27)=ones(16);
A(12:15,12:15)=zeros(4);
SE=strel("diamond",4);
subplot(2,3,1)
showBlue(A, "Original");
subplot(2,3,4)
showRed(double(SE.Neighborhood), "Structuring element");
subplot(2,3,2)
B=imdilate(A,SE);
showCombined(A,B,"Dilation");
subplot(2,3,3)
B=imerode(A,SE);
showCombined(A,B,"Erosion");
subplot(2,3,5)
B=imopen(A,SE);
showCombined(A,B,"Opening");
subplot(2,3,6)
B=imclose(A,SE);
showCombined(A,B,"Closing");
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 10];
print(fig,"morphBinBasicsOps.png",'-dpng');

function showCombined(myA, myB,myTitle)
    %display A over B using transparency
    mySize=size(myA,1);
    zero=zeros(mySize);
    myImgaAlpha=0.2;
    myImgaRGBA=cat(3,zero,zero,myA,myImgaAlpha*myA);
    myImgbAlpha=0.2;
    myImgbRGBA=cat(3,myB,zero,zero,myImgbAlpha*myB);
    myC=myAoverB(myImgaRGBA, myImgbRGBA);
    imAshow(myC,myTitle);
end

function showBlue(myA,myTitle)
    mySize=size(myA,1);
    zero=zeros(mySize);
    myImgaAlpha=0.2;
    myImgaRGBA=cat(3,zero,zero,myA,myImgaAlpha*myA);
    imAshow(myImgaRGBA,myTitle);
end

function showRed(myA,myTitle)
    mySize=size(myA,1);
    zero=zeros(mySize);
    myImgaAlpha=0.2;
    myImgaRGBA=cat(3,myA,zero,zero,myImgaAlpha*myA);
    imAshow(myImgaRGBA,myTitle);
end

% display the RGBA image
% as background we use nontransparent white image
function imAshow(myRGBA, myTitle)
    mySize=size(myRGBA,1);
    one=ones(mySize);
    myWhite=cat(3,one,one,one,one);
    myOut=myAoverB(myRGBA,myWhite);
    if 0
        imshow(myOut(:,:,1:3));
    else
        %better traceable values
        myOut=uint8(myOut*255);
        imshow(myOut(:,:,1:3),[0,255],'InitialMagnification',"fit");
    end
    title(myTitle)
    pixelgrid 
end

%compute A over B for two RGBA images
function vOutImg=myAoverB(imgA, imgB)
    imgA_RGB=imgA(:,:,1:3);
    imgA_alpha=imgA(:,:,4);
    imgB_RGB=imgB(:,:,1:3);
    imgB_alpha=imgB(:,:,4);
    
    alpha_O=imgA_alpha+imgB_alpha.*(1-imgA_alpha);
    vOutImgRGB=(imgA_RGB.*imgA_alpha+imgB_RGB.*imgB_alpha.*(1-imgA_alpha))./alpha_O;
    vOutImgRGB(isnan(vOutImgRGB))=0;
    vOutImg=cat(3,vOutImgRGB,alpha_O);
end

Key part of the program that created Fig. 3

	...
	A= [...
	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
	0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
	0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
	0 1 1 1 1 0 1 1 1 0 1 1 1 1 0
	0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
	0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
	B1= [...
	1 1 1
	1 0 1
	1 1 1];
	B2= 1-B1;
	subplot(2,3,[1 4])
	showBlue(A, 'Original');
	subplot(2,3,2)
	showRed(B1, 'Structuring element B_1');
	subplot(2,3,5)
	showRed(B2, 'Structuring element B_2');
	subplot(2,3,[3 6])
	C=bwhitmiss(A,B1,B2)
	showCombined(A,C, 'HMT');
	...

The source code of the program that created Fig. 5

clear all; close all; clc;
fig=figure;
G= [...
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
F=zeros(size(G,1),size(G,2));
B= [...
     0 1 0
     1 1 1 
     0 1 0];
subplot(2,3,1)
showBW(G, 'Mask');
subplot(2,3,4)
showBW(B, 'Structuring element B');
subplot(2,3,2)
F1=F;F1(2,2)=1;
showBW(F1, 'Marker 1');
subplot(2,3,5)
F2=F;F2(8,2)=1;
showBW(F2, 'Marker 2');
subplot(2,3,3)
R1=imreconstruct(F1,G,B);
showBW(R1, 'Reconstruction 1');
subplot(2,3,6)
R2=imreconstruct(F2,G,B);
showBW(R2, 'Reconstruction 2');
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,"morphBinRecon1.png",'-dpng');
function showBW(myImg, myTitle)

imshow(myImg,'InitialMagnification',"fit");
    title(myTitle)
    pixelgrid 
end

The source code of the program that created Fig. 6

clear all; close all; clc;
fig=figure;
G= [...
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 1 0 1 1 1 0 1 0 0 1 0
    0 1 0 0 1 0 1 0 1 0 1 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
F=zeros(size(G,1),size(G,2));
B= [...
     0 1 0
     1 1 1 
     0 1 0];
subplot(2,3,1)
showBW(G, 'Original image');
subplot(2,3,2)
showBW(B, 'Structuring element B');
subplot(2,3,3)
F(3,3)=1;
showBW(F, 'Marker');
subplot(2,3,4)
showBW(1-G, 'Mask = Original^C');
subplot(2,3,5)
R=imreconstruct(F,1-G,B);
showBW(R, 'Reconstruction');
subplot(2,3,6)
showBW(G+R, 'Filled = Original+reconstruction');

fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,"morphBinRecon2.png",'-dpng');
function showBW(myImg, myTitle)
    imshow(myImg,'InitialMagnification',"fit");
    title(myTitle)
    pixelgrid 
end

The source code of the program that created Fig. 7

clear all; close all; clc;
fig=figure;
A= [...
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 1 0 1 1 1 0 1 0 0 1 0
    0 1 0 0 1 0 1 0 1 0 1 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
subplot(1,3,1)
showBW(1-A, 'Original image');
subplot(1,3,2)
showBW(bwmorph(1-A,'skel',Inf),"bwmorp+skeleton");
subplot(1,3,3)
showBW(bwmorph(1-A,'thin',Inf),"bwmorp+thin");

fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,"morphBinSkel.png",'-dpng');
function showBW(myImg, myTitle)
    imshow(myImg,'InitialMagnification',"fit");
    title(myTitle)
    pixelgrid 
end

The PDF version of this text is available here: morphology_bw_eng.pdf