Optimálne globálne prahovanie
Známou a efektívnou metódou na globálne prahovanie je Otsu metóda [1]. Je optimálna v zmysle, že maximalizuje rozptyl \(\sigma_B^2\) medzi triedami. Algoritmus nie je iteračný, ale je zvyčajne sa na optimalitu preverujú všetky hodnoty prahu. Hľadáme, pre ktorú hodnotu prahu \(T\) je \(\sigma_B^2(T)\) maximálne:
\[ \sigma_B^2(T) = P_1(T)\left( m_1(T) - m_G\right) ) ^2 + P_2(T)\left( m_2(T) - m_G\right) ) ^2\]
kde
\[m_G =\sum_{i=0}^{L-1} i p_i \]
\[m_1 (T)=\frac{1}{P_1 (T)}\sum_{i=0}^T i p_i \]
\[m_2 (T)=\frac{1}{P_2 (T)}\sum_{i=T+1}^{L-1} i p_i \]
kde
\[P_1(T)=\sum_{i=0}^T p_i\]
\[P_2(T)=\sum_{i=T+1}^{L-1} p_i\]
\[p_i=\frac{n_i}{M N}\]
pričom \(n_i\) je počet bodov s úrovňou jasu \(i\), \(L\) je počet úrovní jasu v obraze, \(M, N\) sú rozmery obrazu. Dá sa ukázať, že maximum vždy existuje. Ak je maximum dosahované pre viaceré hodnoty \(T\) za výsledok sa zvykne považovať priemer týchto hodnôt. Odvodenie uvedeného algoritmu a diskusia jeho vlastností je uvedená v [1].
Analogicky sá da odvodiť vzťah pre \(K\) tried, pri ktorých hľadáme \(K-1\) optimálnych prahov \(T_1, ..T_{K-1}\). Vtedy maximalizujeme:
\[ \sigma_B^2 = \sum_{j=1}^{K} P_j\left( m_j - m_G\right) ) ^2\]
kde
\[m_j=\frac{1}{P_j}\sum_{i=T_{j-1}+1}^{T_j} i p_i\]
\[P_j=\sum_{i=T_{j-1}+1}^{T_j} p_i\]
\[p_i=\frac{n_i}{M N}\]
pričom \(n_i\) je počet bodov s úrovňou jasu \(i\), \(L\) je počet úrovní jasu v obraze, \(M, N\) sú rozmery obrazu a \(T_0=-1, T_K=L-1\)
V prostredí MATLAB je Otsu prahovanie implementované pomocou funkcie graythresh (argument je obraz) a otsuthresh (argument sú počty bodov \(n_i\) s úrovňou jasu \(i\)) - pre dve triedy a multithresh – pre viac tried.
Príklad použitia Otsu prahovania je na Obr. 1. Úlohou je nájsť optimálny prah medzi dvomi triedami. Vidíme ako prítomnosť silnejšieho šumu môže sťažiť určenie prahu.
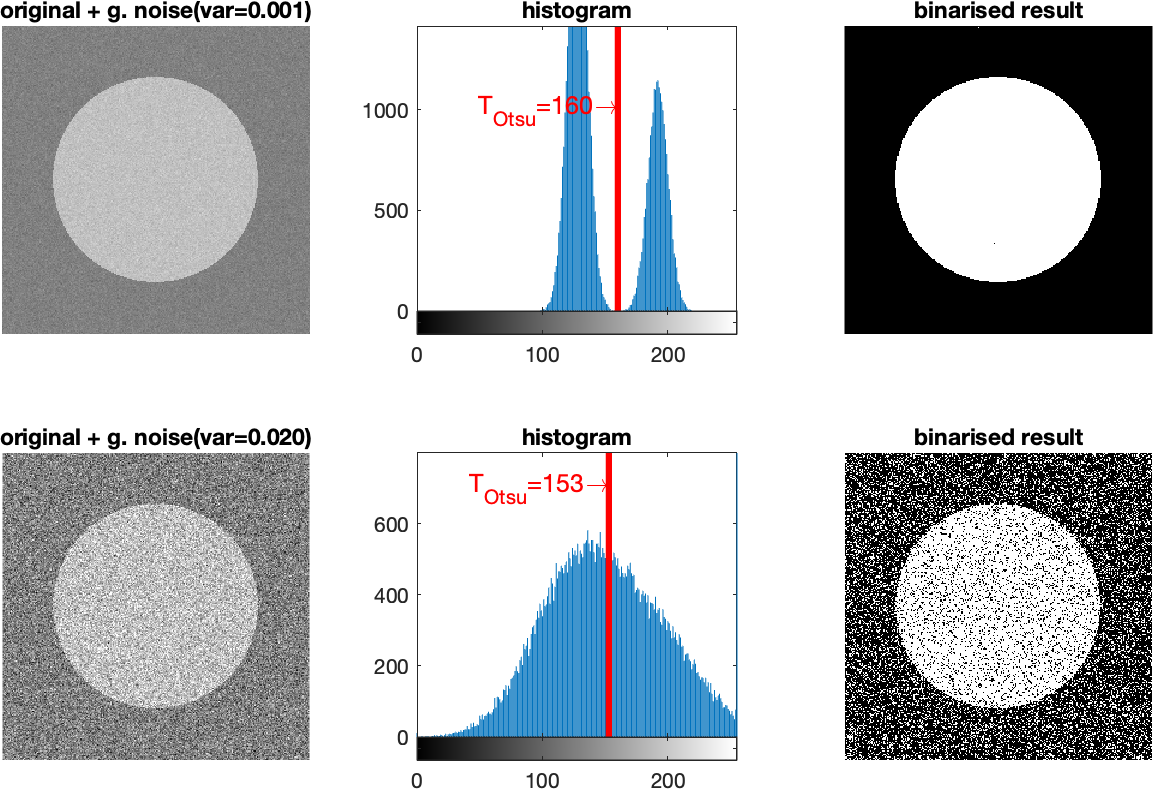
Obr. 1 Príklad Otsu prahovania pri zašumenom vstupnom signáli. V hornom riadku je slabšie zašumený signál, v dolnom silnejšie.
Referencie
[1] Gonzalez, R., C., Woods, E., W., Digital Image Processing, Global Edition, 4th edition, Pearson 2018, ISBN 10: 1-292-22304-9
Prílohy
Zdrojový kód programu, ktorý vytvoril Obr. 1
clear all; close all; clc;
N=256
mtx=uint8(128*ones(N,N));
imshow(mtx,[0,255]);
h = drawcircle('Center',[N/2 N/2],"Radius",N/3);
mask = createMask(h);
mtx(mask>0)=128+64;
fig=figure
subplot(2,3,1)
myvar=0.001
mtxn = imnoise(mtx,'gaussian',0,myvar);
imshow(mtxn,[0,255]);
title(sprintf("original + g. noise(var=%.3f)",myvar))
subplot(2,3,2)
imhist(mtxn);
hold on
[T,EM] = graythresh(mtxn)
myT=T*255;
myYlim=ylim;
plot([myT myT],[myYlim(1) myYlim(2)],"red","LineWidth",3)
text(myT,1000,sprintf("T_{Otsu}=%.0d\\rightarrow",myT),...
'HorizontalAlignment','right',"FontSize",12,"Color","red")
title("histogram")
subplot(2,3,3)
BW = imbinarize(mtxn,T);
imshow(BW);
title("binarised result")
subplot(2,3,4)
myvar=0.2
mtxn = imnoise(mtx,'gaussian',0,myvar);
imshow(mtxn,[0,255]);
title(sprintf("original + g. noise(var=%.3f)",myvar))
subplot(2,3,5)
imhist(mtxn);
hold on
[T,EM] = graythresh(mtxn)
myT=T*255;
myYlim=ylim;
plot([myT myT],[myYlim(1) myYlim(2)],"red","LineWidth",3)
text(myT,700,sprintf("T_{Otsu}=%i\\rightarrow",myT),...
'HorizontalAlignment','right',"FontSize",12,"Color","red")
title("histogram")
subplot(2,3,6)
BW = imbinarize(mtxn,T);
imshow(BW);
title("binarised result")
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 10 6];
print(fig,"segmOtsuNoise.png",'-dpng');
PDF verzia tejto stránky je dostupná tu: segmentation_otsu_sk.pdf