Zošívanie obrazu
Pri snímaní obrazu niekedy nasáva situácia, že naše snímacie zariadenie celú scénu nedokáže pokryť. Jedným z riešení je zosnímať jednotlivé časti scény a potom tie časti zložiť dokopy do výslednej scény tak aby nebolo vidieť že výsledný obraz je zložený z viacerých. Tento proces sa nazýva zošívanie obrazu. V ňom tvoríme výsledný obraz z dlaždíc jednotlivých dielčích obrazov. Tieto dlaždice musia navzájom "pasovať" a miesto, kde boli zošité by nemalo byť vidieť. Táto úloha nie je triviálna vzhľadom na to, nesnímame z toho istého bodu v tom istom čase a kraje obrazov nevieme často trafiť tak presne aby obrazy na seba plynulo nadväzovali. Pridávajú sa k tomu geometrické nedokonalosti snímača a ďalšie okolnosti. Ak vieme, že výslednú scénu budeme zošívať tak pri snímaní dielčích častí je vhodné:
- snímať za tých istých vonkajších podmienok, tak aby sa scéna menila minimálne (poloha objektov, osvetlenie), t.j. spravidla čo najrýchlejšie
- snímať pri tých istých vnútorných podmienok, t.j. parametroch snímača (vypnúť automatické nastavovania parametrov snímania, autofokus, nemeniť nastavenia, ...)
- mať prekryv dielčích častí minimálne 20-30\% aby bol dostatočný priestor na zošitie
V princípe sa môžeme pozerať na zošívanie obrazu ako na vytváranie panorámy (obrazu okolia pozorovateľa). Dva základné druhy panorámy sú rotačná a translačná. Ak sa pozorovateľ nehýbe z miesta (iba otáča a pozerá okolo seba) hovoríme o rotačnej panoráme. Ak sa neotáča ale hýbe a pozerá stále jedným smerom (napr cez okno auta ktoré ide po ulici) hovoríme o translačnej panoráme. Z týchto základných druhov sa za jednoduchší problém dá považovať rotačná panoráma, lebo tá skladá okolie tak ako vyzerá z jedného bodu, čo ma jednoznačné riešenie (v zidealizovanom prípade). Keď sa pozorovací bod hýbe a sleduje tú istú oblasť priestoru, tá sa môže vyzerať z rôznych pozorovacích bodov rôzne - iné odlesky, iný tvar (pozeráme sa spravidla na trojrozmernú oblasť). Ak by sme pri pohybe sledovali len oblasť kolmo na smer pohybu (tak ako napr. scanner) tak už obraz jednoznačný je, ale potrebujeme veľa snímkov. Obraz je jednoznačná aj keď scéna je plochá, bez odleskov a podobne. Základná situácia pri pri snímaní zdrojových snímok pre translačnú a rotačnú panorámu su zobrazená na Obr. 1.
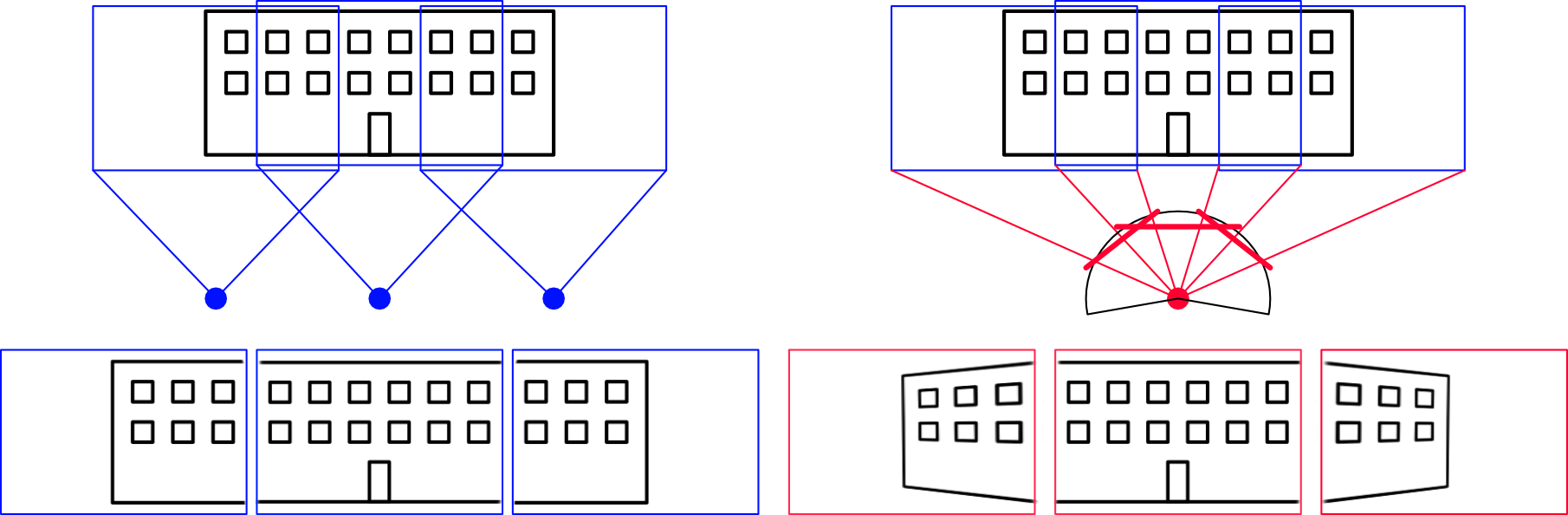
Obr. 1 Schematické naznačenie snímania pri tvorbe translačnej (vľavo)a rotačnej (vpravo) panorámy.
Pri rotačnej panoráme ak objekty nie sú v rovnakej vzdialenosti od pozorovateľa vidíme pri bočných pohľadoch vplyv perspektívy - pôvodne rovnobežné hrany budovy smerujú k sebe. Pri zošívaní toto treba zohľadniť. Príklad zošívanie pri rotačnej panoráme, kde sa snažíme zachovať geometriu centrálneho obrazu je znázornený na Obr. 2. Vidíme, že ak ako centrálny zvolíme (správne) tretí obrázok v sekvencii, a k nemu prišívame okolité obrázky tak krajné obrázky musíme čoraz viac vertikálne naťahovať. Výsledný obraz ma tvar motýlích krídel. A ak zvolíme ako centrálny obrázok nesprávny obrázok, tak pri korekcii vplyvu perspektívy bude celý obraz do šikma.

Obr. 2 Príklad zošívania rotačnej panorámy. Zosnímaná sekvencia obrázkov je hore, v strede zošitá panoráma, keď ako východzí obrázok bol zvolený ľavý a dole, keď ako východzí obrázok bol zvolený ten stredný. Pri zošívaní boli použité: SURF na detekciu kľúčových bodov, MSAC na nájdenie projektívnej transformácie, binárne zmiešavanie pomocou alfa kanálu.
Algoritmus zošívania musí riešiť viaceré problémy:
- Zvoliť cieľovú projekciu (plochú cylindrickú, sférickú) - na akom povrchu budeme výsledok konštruovať.
- Zistiť ako sa obrázky prekrývajú. De facto sa vykoná registrácia obrazu - mapovanie obrazov do spoločného súradnicového systému. Spravidla sa jeden zvolí ako centrálny a k nemu sa hľadá transformácia okolitých obrazov, aby sa čo najlepšie prekryli.
- Určenie hranice medzi zošívanými obrázkami - kadiaľ pôjde šev. Triviálna voľba je po hrane obrázku ale sofistikovanejšie metódy hľadajú, kde sa obrazy čo najviac zhodujú a šev vedú tadiaľ. Prípadne sa šije pozdĺž hrán, kde je šev dobre vizuálne zamaskovaný.
- Voľba metódy zmiešavania - triviálna a intuitívna metóda je použiť pixely jedného obrázku na jednej strane švu a pixely druhého obrázku na druhej strane švu. Prípadne sa v okolí švu môžu hodnoty priemerovať či váhovať, použiť zmiešavanie na základe priesvitnosti (alpha blending) či zmiešavanie pomocou Laplaceovských pyramíd, prípadne využiť princíp zmiešavania ako pri tvorbe obrazu z vysokým dynamickým rozsahom.
Detaily toho ako postupne prebiehalo zošívanie obrázku v dolnej časti Obr. 2 sú ukázané na Obr. 3

Obr. 3 Príklad priebehu zošívania, v hornom riadku vidíme originály, pod nimi ich registrované verzie, pod nimi binárnu masku, ktorá určí ktoré ich pixely sa použijú (vidíme, ze sa použijú všetky pixely, teda šev ich po ich ľavej hrane, na spodku stav celkovej panorámy po prišití obrazu v danom kroku)
Pri zošívaní na Obr. 2 bol konkrétny zošívací algoritmus nasledovný [1]:
- Zvoľ sieľovú projektciu: rovná plocha
- Označ obrázky ako \(I(1), ...I(5)\)
- Pre každú dvojicu obrazu \(I(n), ...I(n-1)\) vykonaj registráciu, nájdi transformáciu \(I(n)\) do súradnicového systému \(I(n-1)\)
- Pomocou metódy SURF identifikuj význačné body na \(I(n)\) aj \(I(n-1)\) . MATLAB : detectSURFFeatures() + extractFeatures()
- Hľadaj medzi nimi jedinečné páry s najlepšou zhodou (MATLAB: matchFeatures(), s voľbou "Unique") na základe metriky SAD (Sum of Absolute Differences)
- Na základe párov bodov odhadni transformáciu \(I(n)\) do súradnicového systému \(I(n-1)\) pomocou metódy MSAC (M-estimator sample consensus) ktorá je variantom známej metódy RANSAC (random sample consensus), pričom sa hľadá projektívna transformácia (MATLAB: estgeotform2d() s parametrom "projective")
- vypočítaj výslednú transformáciu \(I(n)\) voči počiatočnému \(I(1)\) ako \(\prod_{n=1}^n T(n)\)
- Ak je centrálny obraz iný ako \(I(1)\) prepočítaj\(T(n)\) voči tomuto obrazu
- K \(I(1)\) postupne pre prišívaj ďalšie obrázky, pričom ako šev použi transformovanú hranu prišívaného obrazu a použi najjednoduchšie zmiešavanie t.j. priši rovno plné hodnoty pixelov v oblasti nového obrazu (MATLAB: vision.AlphaBlender, pričom operácia je "Binary mask")
Na rozdiel od situácie na Obr. 2, kde zošívanie prebiehalo horizontálne, v reálnych panorámach sa často zošíva aj v druhom smere, teda výsledný obraz je tvorený napr. z 20x10 vstupných prekrývajúcich sa obrazov. Na zošívanie obrazu existuje množstvo špecializovaných programov (výborný prehľad je uvedený napr. v [2])
Referencie
[1] Mathworks, Feature Based Panoramic Image Stitching, http://www.mathworks.com/help/vision/ug/feature-based-panoramic-image-stitching.html
[2] Comparison of photo stitching software, wikipedia, https://en.wikipedia.org/wiki/Comparison_of_photo_stitching_software#:~:text=Photo%20stitching%20software%20produce%20panoramic,more%20or%20less%20smooth%20image.
Prílohy
Zdrojový kód programu, ktorý vytvoril Obr. 2 aj Obr. 3
clear all;close all;clc; %https://www.mathworks.com/help/vision/ug/feature-based-panoramic-image-stitching.html % Load images. buildingDir = fullfile(toolboxdir('vision'),'visiondata','building'); buildingScene = imageDatastore(buildingDir); [tforms,imageSize]=getTformsSizes(buildingScene); panorama0=getPanorama(buildingScene,tforms,imageSize,0); panorama1=getPanorama(buildingScene,tforms,imageSize,1); fig=figure; subplot(5,1,[1 1]); montage(buildingScene.Files,"Size",[1 5], "BorderSize", [2 2],"BackgroundColor","w"); subplot(5,1,[2 3]); imshow(panorama0) subplot(5,1,[4 5]); imshow(panorama1) fig.PaperUnits = 'inches'; fig.PaperPosition = [0 0 10 12]; print(fig,"stitching.png",'-dpng'); %========================================================= function [tforms,imageSize]=getTformsSizes(buildingScene) % Read the first image from the image set. I = readimage(buildingScene,1); % Initialize features for I(1) grayImage = im2gray(I); points = detectSURFFeatures(grayImage); [features, points] = extractFeatures(grayImage,points); % Initialize all the transformations to the identity matrix. Note that the % projective transformation is used here because the building images are fairly % close to the camera. For scenes captured from a further distance, you can use % affine transformations. numImages = numel(buildingScene.Files); tforms(numImages) = projtform2d; % Initialize variable to hold image sizes. imageSize = zeros(numImages,2); % Iterate over remaining image pairs for n = 2:numImages % Store points and features for I(n-1). pointsPrevious = points; featuresPrevious = features; % Read I(n). I = readimage(buildingScene, n); % Convert image to grayscale. grayImage = im2gray(I); % Save image size. imageSize(n,:) = size(grayImage); % Detect and extract SURF features for I(n). points = detectSURFFeatures(grayImage); [features, points] = extractFeatures(grayImage, points); % Find correspondences between I(n) and I(n-1). indexPairs = matchFeatures(features, featuresPrevious, 'Unique', true); matchedPoints = points(indexPairs(:,1), :); matchedPointsPrev = pointsPrevious(indexPairs(:,2), :); % Estimate the transformation between I(n) and I(n-1). tforms(n) = estgeotform2d(matchedPoints, matchedPointsPrev,... 'projective', 'Confidence', 99.9, 'MaxNumTrials', 2000); % Compute T(1) * T(2) * ... * T(n-1) * T(n). tforms(n).A = tforms(n-1).A * tforms(n).A; end end %========================================================= function panorama = getPanorama(buildingScene,tforms,imageSize,doCentering) if(doCentering) % Compute the output limits for each transformation. for i = 1:numel(tforms) [xlim(i,:), ylim(i,:)] = outputLimits(tforms(i), [1 imageSize(i,2)], [1 imageSize(i,1)]); end avgXLim = mean(xlim, 2); [~,idx] = sort(avgXLim); centerIdx = floor((numel(tforms)+1)/2); centerImageIdx = idx(centerIdx); Tinv = invert(tforms(centerImageIdx)); for i = 1:numel(tforms) tforms(i).A = Tinv.A * tforms(i).A; end end for i = 1:numel(tforms) [xlim(i,:), ylim(i,:)] = outputLimits(tforms(i), [1 imageSize(i,2)], [1 imageSize(i,1)]); end maxImageSize = max(imageSize); % Find the minimum and maximum output limits. xMin = min([1; xlim(:)]); xMax = max([maxImageSize(2); xlim(:)]); yMin = min([1; ylim(:)]); yMax = max([maxImageSize(1); ylim(:)]); % Width and height of panorama. width = round(xMax - xMin); height = round(yMax - yMin); % Initialize the "empty" panorama. I = readimage(buildingScene,1); panorama = zeros([height width 3], 'like', I); blender = vision.AlphaBlender('Operation', 'Binary mask', ... 'MaskSource', 'Input port'); % Create a 2-D spatial reference object defining the size of the panorama. xLimits = [xMin xMax]; yLimits = [yMin yMax]; panoramaView = imref2d([height width], xLimits, yLimits); numImages = numel(buildingScene.Files); % Create the panorama. for i = 1:numImages; I = readimage(buildingScene, i); imwrite(I,sprintf("img%02i.png",0*5+i)); % Transform I into the panorama. warpedImage = imwarp(I, tforms(i), 'OutputView', panoramaView); imwrite(warpedImage,sprintf("img%02i.png",1*5+i)); % Generate a binary mask. mask = imwarp(true(size(I,1),size(I,2)), tforms(i), 'OutputView', panoramaView); imwrite(mask,sprintf("img%02i.png",2*5+i)); % Overlay the warpedImage onto the panorama. panorama = step(blender, panorama, warpedImage, mask); imwrite(panorama,sprintf("img%02i.png",3*5+i)); end fig=figure imds = imageDatastore(fullfile(".","img*")); montage(imds,"Size", [4 5],"BorderSize", [1 1],"BackgroundColor","w") print(fig,sprintf("stitchingDetailsDC%u.png",doCentering),'-dpng'); end
PDF verzia tejto stránky je dostupná tu:stitching_sk.pdf