Morfológia s šedotónovým obrazom
Okrem čiernobieleho obrazu je morfológia veľmi užitočná aj pri spracovaní šedotónového obrazu. Používajú sa všetky 4 základné operácie erózia, dilatácia, otvorenie, zatvorenie. Pri voľbe štrukturálneho elementu máme na výber, či chceme použiť plochý (z konštantnou hodnotou intenzity), alebo neplochý.
Nech \(f(x,y)\) je obraz a \(b(x,y)\) štrukturálny element. Potom erózia \(f(x,y)\) pri použití \(b(x,y)\) je definovaná ako
- pri plochom štrukturálnom elemente sú nové hodnoty obrazu minimá z okolia daného elementu
\[ \left[ f\ominus b\right] (x,y)=\min_{(s,t)\in b} \left\lbrace f(x+s, y+t) \right\rbrace \]
- pri neplochom štrukturálnom elemente \(b_N\)je braná do úvahy aj hodnota elementu
\[ \left[ f\ominus b_N\right] (x,y)=\min_{(s,t)\in b} \left\lbrace f(x+s, y+t) -b_N(s,t) \right\rbrace \]
Podobne dilatácia je definovaná ako
- pri plochom štrukturálnom elemente sú nové hodnoty obrazu maximá z okolia otočeného daného elementu
\[ \left[ f\ominus b\right] (x,y)=\max_{(s,t)\in b} \left\lbrace f(x-s, y-t) \right\rbrace \]
- pri neplochom štrukturálnom elemente \(b_N\)je braná do úvahy aj hodnota elementu
\[ \left[ f\ominus b_N\right] (x,y)=\max_{(s,t)\in b} \left\lbrace f(x-s, y-t) -\widehat{b_N}(s,t) \right\rbrace \]
Otvorenie a zatvorenie je definované pomocou dilatácie a erózie rovnako ako tomu je pri čiernobielom obraze. V prostredí MATLAB sa jedná o tie isté funkcie: imdilate, iimerode, imopen, imclose. Príklady všetkých uvedených operácií sú na Obr. 1.
Ďaľšou operáciou je morfologické vyhladzovanie. Je to kombinácia otvorenia a následného zatvorenia. Príklad tejto operácie je uvedený na Obr. 2.
Zaujímavou operáciou je morfologický gradient (MG), pri kotorm sa od dilatovaného obrazu odčítava erodovaný (čo by malo zvýrazniť ohraničenie objektov):
\[I_{MG}=(A\oplus B)- (A\ominus B)\]
Príklad tejto operácie je uvedený na Obr. 3.
Šedotónová morfológia môže byť použitá aj ako predspracovanie pred segmentáciou. Napr. operácia top-hat sa používa na zrovnomernenie osvetlenia scény pred globálnou segmentáciou:
\[I_{TH}= I - (I \circ B)\]
Príklad tejto operácie je uvedený na Obr. 4.
Top-hat operácia sa dá využiť aj na detekciu blobov. Využíva sa pri tom vlastnosť, že ak veľkosť blobu a štrukurálneho elementu je podobná, tak bloby v obraze pri odčítania otvorenia stmavnú. Vieme teda zostrojiť graf jasu obrazu po toop-hat operácii v závislosti od veľkosti použitého Štrukturálneho elementu. Lepšie je zobrazit prvú deriváciu (gradient). Tam stačí hľadať maximálnu hodnotu a na základe toho určiť či v obraze sú bloby a akú majú veľkosť. Príklad takéhoto využitia top-hat je znázornený na Obr. 5. Ak pracujeme s nevyhladenou verziou obrázku (hore), potom maximum zmeny jasu je kvôli šumu prítomný pri malých hodnotách veľkosti štrukturálneho elementu. Na vyhladenej verzii obrázku vidíme maximálne hodnoty gradientov zmien jasu otvorení pri veľkostiach štrukturálneho elementu 19 a 27.

Obr. 1 Príklady základných morfologických operácií erózia, dilatácia, otvorenie, zatvorenie pre šedotónový obraz.

Obr. 2 Príklady morfologického vyhladzovania a porovnanie s mediánovým filtrom.

Obr. 3 Príklady morfologického gradientu a porovnanie s LoG filtrom.
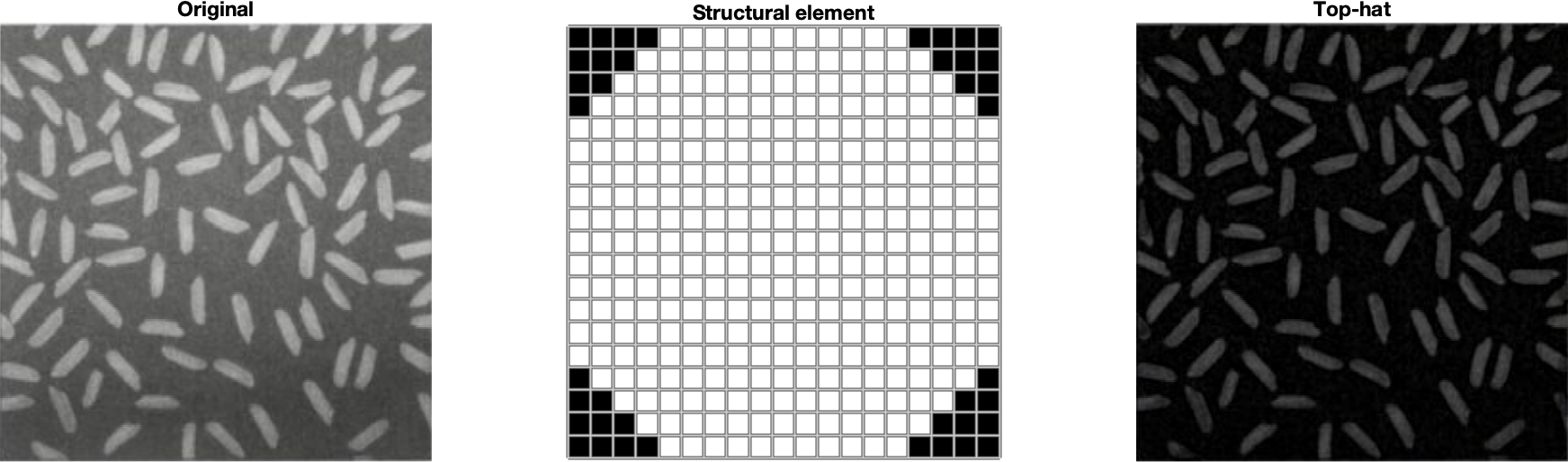
Obr. 4 Príklad použitia top-hat operácie na zrovnomernenie osvetlenia scény
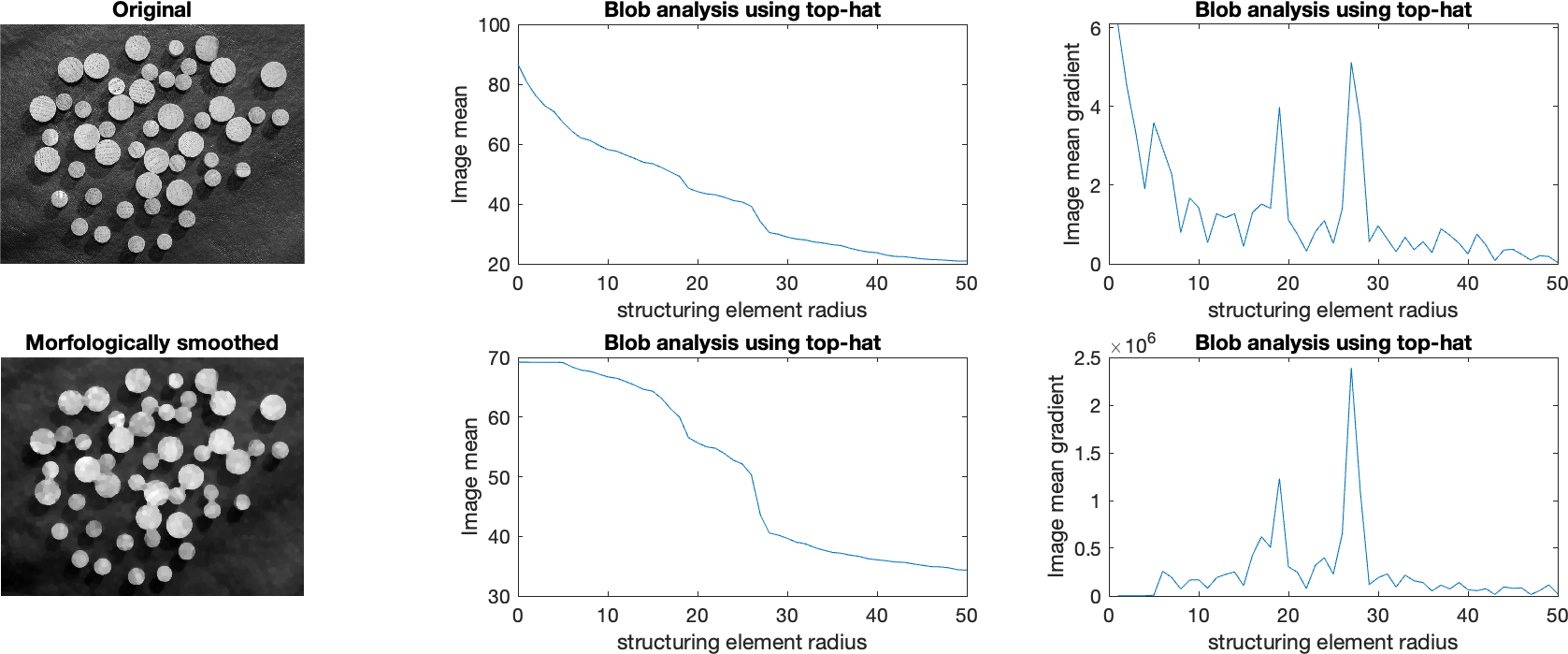
Obr. 5 Príklad použitia opakovanej top-hat operácie na detekciu blobov.
Viac informácii o morfologických operáciách na šedotónovom obaze je možné nájsť v [1] [2] [3].
Referencie
[1] Mathworks, Morphological Operations, online: https://www.mathworks.com/help/images/morphological-filtering.html
[2] Gonzalez, R., C., Woods, E., W., Digital Image Processing, Global Edition, 4th edition, Pearson 2018, ISBN 10: 1-292-22304-9
[3] Gonzalez, R., C., Woods, E., W., Eddings, S., L., Digital Image Processing using MATLAB, Gatesmark Publishing, ISBN-10: 0-9820854-1-9
Prílohy
Zdrojový kód programu, ktorý vytvoril Obr. 1
clear all; close all; clc;
fig=figure;
A=im2gray(imread('baboon.png'));
subplot(2,3,1)
showCol(A,'Original');
subplot(2,3,4)
B=strel('disk',4);
showCol(B.Neighborhood,'Structuring element, r=4')
pixelgrid;
subplot(2,3,2)
C=imerode(A,B);
showCol(C,'Erosion')
subplot(2,3,3)
C=imdilate(A,B);
showCol(C,'Dilation')
subplot(2,3,5)
C=imopen(A,B);
showCol(C,'Opening')
subplot(2,3,6)
C=imclose(A,B);
showCol(C,'Closing')
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 10];
print(fig,'morphGrayBasicOps.png','-dpng');
function showCol(myImg, myTitle)
imshow(myImg);
title(myTitle)
end
Zdrojový kód programu, ktorý vytvoril Obr. 2
clear all; close all; clc;
fig=figure;
ORIG= imread('cameraman.tif');
SP = imnoise(ORIG,'salt & pepper');
subplot(2,3,1);
imShowTit(SP,"Image + Salt&pepper noise")
subplot(2,3,4);
MF=medfilt2(SP);
imShowTit(MF, "median filter applied")
subplot(2,3,2);
SE = strel("disk",1);
imShowTit(double(SE.Neighborhood), "Structural element A")
pixelgrid;
subplot(2,3,5);
OP=imopen(SP,SE);
CL=imclose(OP,SE);
imShowTit(CL, "Morph. smoothing A")
subplot(2,3,3);
SE = strel("disk",2);
imShowTit(double(SE.Neighborhood), "Structural element B")
pixelgrid;
subplot(2,3,6);
OP=imopen(SP,SE);
CL=imclose(OP,SE);
imShowTit(CL, "Morph. smoothing B")
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 10];
print(fig,'morphGrayBasicSmooth.png','-dpng');
function imShowTit(myImg, myTitle)
imshow(myImg);
title(myTitle)
end
Zdrojový kód programu, ktorý vytvoril Obr. 3
clear all; close all; clc;
fig=figure;
SP= imread('cameraman.tif');
subplot(2,3,1);
imShowTit(SP,'Original')
subplot(2,3,4);
myFilt = fspecial('log',10,2);
myLog=imfilter(SP,myFilt);
imShowTit(myLog,'LoG, \sigma=2')
subplot(2,3,2);
SE = strel('disk',1);
imShowTit(double(SE.Neighborhood), 'Structural element A')
pixelgrid;
subplot(2,3,5);
CL=imdilate(SP,SE)-imerode(SP,SE);
imShowTit(CL, 'Morph. gradient A')
subplot(2,3,3);
SE = strel('disk',2);
imShowTit(double(SE.Neighborhood), 'Structral element B')
pixelgrid;
subplot(2,3,6);
CL=imdilate(SP,SE)-imerode(SP,SE);
imShowTit(CL, 'Morph. gradient B')
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 10];
print(fig,'morphGrayBasicGrad.png','-dpng');
function imShowTit(myImg, myTitle)
imshow(myImg,[]);
title(myTitle)
end
Zdrojový kód programu, ktorý vytvoril Obr. 4
clear all; close all; clc;
fig=figure;
SP= imread('rice.png');
subplot(1,3,1);
imShowTit(SP,'Original')
subplot(1,3,2);
SE=strel("disk",10);
imShowTit(double(SE.Neighborhood), "Structural element")
pixelgrid;
subplot(1,3,3);
CL=imtophat(SP,SE);
imShowTit(CL,'Top-hat')
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,'morphGrayBasicTopHat.png','-dpng');
function imShowTit(myImg, myTitle)
imshow(myImg,[]);
title(myTitle)
end
Zdrojový kód programu, ktorý vytvoril Obr. 5
clear all; close all; clc;
fig=figure;
f = im2gray(imread("dowels2.tif"));
subplot(2,3,1)
imShowTit(f,'Original')
subplot(2,3,4)
%vyhladenie
se = strel('disk',5);
fo = imopen(f,se);
fx = imclose(fo,se);
imShowTit(fx, 'Morfologically smoothed');
subplot(2,3,2)
N=50
sumpixels = zeros(1,N+1);
for k = 0:N
se = strel("disk",k);
fy = imopen(f,se);
sumpixels(k + 1) = sum(fy(:));
end
plot(0:N, sumpixels/(size(f,1)*size(f,2))), xlabel("structuring element radius"), ylabel("Image mean")
title("Blob analysis using top-hat")
subplot(2,3,3)
plot(-diff(sumpixels/(size(f,1)*size(f,2))))
xlabel("structuring element radius")
ylabel("Image mean gradient")
title("Blob analysis using top-hat")
subplot(2,3,5)
N=50
sumpixels = zeros(1,N+1);
for k = 0:N
se = strel("disk",k);
fy = imopen(fx,se);
sumpixels(k + 1) = sum(fy(:));
end
plot(0:N, sumpixels/(size(f,1)*size(f,2))), xlabel("structuring element radius"), ylabel("Image mean")
title("Blob analysis using top-hat")
subplot(2,3,6)
plot(-diff(sumpixels))
xlabel("structuring element radius")
ylabel("Image mean gradient")
title("Blob analysis using top-hat")
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,'morphGrayBasicBlob.png','-dpng');
function imShowTit(myImg, myTitle)
imshow(myImg,[]);
title(myTitle)
end
PDF verzia tejto stránky je dostupná tu: morphology_gray_sk.pdf