DIP:  Morfológia s čiernobielym obrazom

V tejto časti si uvedieme základné definície a operácie morfológiu s čiernobielym (t.j. binárnym) obrazom. Nech \(E\) je euklidovský priestor \(Z^2\). T.j. je to priestor všetkých celočíselných dvojíc čísel. Nech \(B\) je množina bodov z \(E\), napr.: \(B\)={(-1,0), (0,-1), (0,0), (0,1), (1,0)}. Potom transláciou množiny \(B\) o vektor \(z\) nazývame množinu \(B_z\), pre ktorú platí:

\[B_z=\{b+z | b \in B\}, \forall z \in E\]

Zrkadlením množiny \(B\) označujeme množinu \(\hat{B}\), pričom platí:

\[\hat{B}=\{x \in E | -x \in B\}\]

Nech \(A\) je čiernobiely obraz - množina bodov \(A\) v priestore \(E\) ktorej priradíme obdĺžnikové ohraničenie. Pod štrukturálnym elementom budeme rozumieť takú množinu \(B\), ktorej priradíme stred v bode \(0,0\). Potom eróziou obrazu \(A\) pomocou štrukturálneho elementu \(B\) nazývame množinu:

\[A\ominus B=\{z \in E | B_z \subseteq A\}\}\]

T.j. je to množina bodov, kam sa dostane stred \(B\), keď sa množina \(B\) posúva v rámci množiny \(A\).

Dilatáciou obrazu \(A\) pomocou štrukturálneho elementu \(B\) nazývame množinu:

\[A\oplus B=\{z \in E | \{\hat{B}_z \cap A \neq \emptyset\}\}\]

T.j. je to množina bodov, kam sa dostane stred \(B\), keď sa množina \(B\) posúva tak, že sa ešte aspoň čiastočne prekrýva s \(A\).

Otvorením obrazu \(A\) pomocou štrukturálneho elementu \(B\) nazývame množinu:

\[ A \circ B = ( A \ominus B) \oplus B\]

T.. je to množina bodov, kam sa dostanú body \(B\), keď sa množina \(B\) posúva v rámci množiny \(A\)..

Zatvorením obrazu \(A\) pomocou štrukturálneho elementu \(B\) nazývame množinu:

\[ A \bullet B = ( A \oplus B) \ominus B\]

T.. je to množina bodov, kam sa nedostanú body \(B\), keď sa množina \(B\) posúva tak, že sa ešte neprekrýva s \(A\).

Erózia s dilatácia ako aj otvorenie so zatvorením sú komplementárne operácie. Označme pomocou \(^C\) komplementárnu množinu. Potom platí:

\[(A\ominus B)^C = A^C \oplus \hat{B}\]

\[(A\oplus B)^C = A^C \ominus \hat{B}\]

\[(A\circ B)^C = A^C \bullet \hat{B}\]

\[(A\bullet B)^C = A^C \circ \hat{B}\]

V prostredí MATLAB sa realizujú pomocou funkcií imerode, imdilate, imopen, imclose. Štrukturálny element sa vytvára pomocou funkcie strel a je to obdĺžniková oblasť. Komplementárny obraz sa dá získať pomocou funkcie imcomplement. Viac informácií možno nájsť v [1]. Príklady uvedených základných morfologických operácií pre čiernobiely obraz sú uvedené na Obr. 1.

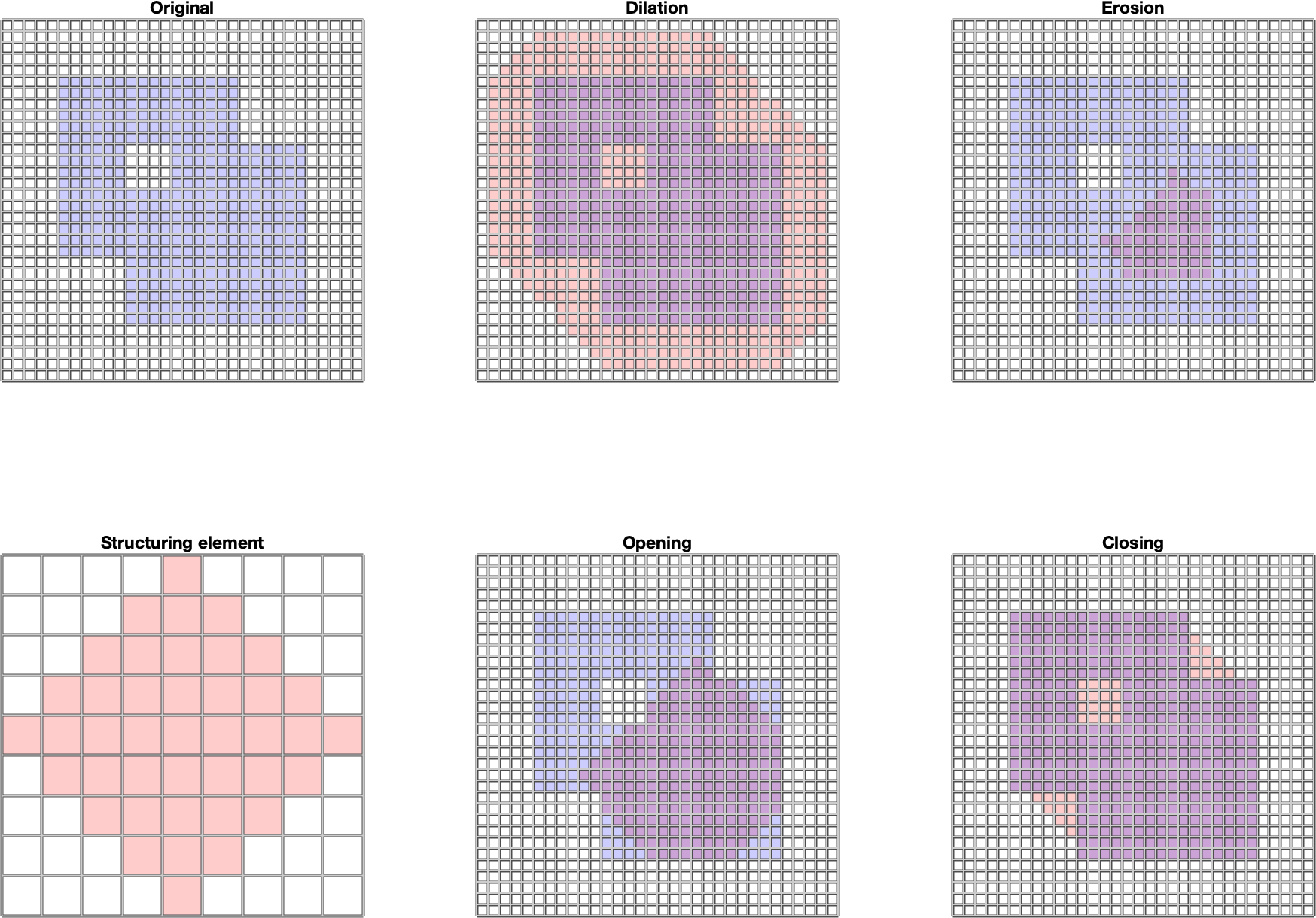
Obr. 1 Príklady základných morfologických operácií erózia, dilatácia, otvorenie, zatvorenie pre čiernobiely obraz. Pre názornosť sú originálny obraz, štrukturálny element a výsledok morfologickej operácie farebne odlíšené pomocou červeného a modrého farebného kanála a je použité zmiešavanie pomocou alfa kanálu.

Základné morfologické operátory umožnujú detekovať hranice objektu pomocou operácie:

\[A-A\ominus B\]

T.j. od originalneho obrazu odčítame jeho zerodovanú verziu, takže nám ostane okraj. Príklady využitia je uvedený na Obr. 2

Pokročilejšou morfologickou operáciou používanou pri rozpoznávaní tvarov je hit or miss transformácia (HMT). Táto operácia pracuje s dvomi štrukúrnymi elementami \(B_1, B_2\). Výsledkom je množina:

\[A \circledast B_{1,2}=(A\ominus B_1)\cap(A^C \ominus B_2) \]

Táto operácia umožňuje interpretovať body neprítomné v obraze a štrukturálnom elementa ako pozadie. Ak zvolíme \(B_2=B_1^C\), t.j. \(B_2\) reprezentuje pozadie a \(A\) s \(A^C\) tiež interpretujeme ako popredie a pozadie, potom výsledkom HMT sú polohy stredu strukturálneho elementu \(B_1\), kde jeho popredie je v popredí \(A\) a zároveň jeho pozadie je v pozadí \(A\). V prostredí MATLAB je HMT dostpná pomocou funkcie bwhitmiss. Príklad HMT je uvedený na Obr. 3. HMT nám umožnuje okrem popredia a pozadia definovať, na ktorých bodoch nám nezáleží. To sú tie, ktoré sa nevyskytujú ani v \(B_1\), ani v \(B_2\). Príklad na využitie takýchto štrukturych elementov je Obr. 4.

Morfologická rekonštrukcia je iteračná metóda na rekonštrukciu oblastí., ktorá používa 2 obrázky a štrukturálny element. Prvý obrázok (marker - \(F\)) určuje štartovací bod (body), druhý určuje cieľovú oblasť (maska - \(G\)). Štrukturálny element \(B\) určuje konektivitu. Rekonštrukcia sa označuje \(R_G^F\) a počíta sa nasledovne:

Inicializuj \(h_1=F\)
Opakuj \(h_{k+1}=(h_k\oplus B) \cap G\) až kým nebude platiť \(h_{k+1}=h_k\)
Výstupom je \(R_G^F=h_{k}\)

Ak je viac objektov v obraze, dajú sa podľa morfologickej rekonštrukcie oddeliť (zakaždným markerom určíme iný objekt). Prípadne sa dajú týmto algoritmom zapĺňať prázdne ohraničené oblasti ( ak \(A\) je oblasť, potom ako masku zvolíme \(A^C\)). V prostredí MATLAB je rekonštrukcia dostupná pomocou funkcie imreconstruct. Príklady oboch využití sú na Obr. 5 a 6. Morfologickú rekonštrukciu používa aj funkcia imfill.

Pri spracovaní obrazu môže byť užitočné získať kostra (skeleton) určenej oblasti. Kostra je prepojená množina bodov ktoré sú ekvidištančne vzdialené od okraja oblasti. Morfologicky sa táto množina dá získať pomocou opakovaného ztenšovania (thinning) oblasti napr. pomocou erózie, pričom sa zachovávajú koncové body a líniová konektivita (hovoríme aj o topologicky zachovávajúcom ztenšovaní). V prostredí MATLAB je táto operácia dostupná pomocou funkcie bwmorph, pričom ako operácie je zvolená "thin", resp. "skel" (používa algoritmus [4]). Operácie dávajú mierne odlišný vysledok. Príklad je uvedený na Obr. 7.

Obr. 2 Príklad detekcie hraníc objektu pomocou morfologických operácií pre čiernobiely obraz. Pre názornosť sú originálny obraz, štrukturálny element a výsledok morfologickej operácie farebne odlíšené pomocou červeného a modrého farebného kanála a je použité zmiešavanie pomocou alfa kanálu.

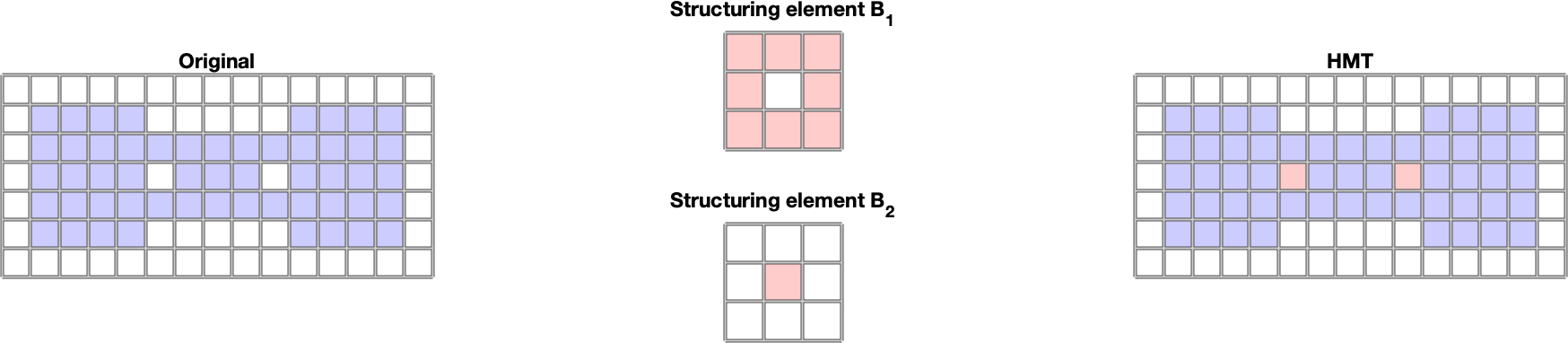
Obr. 3 Príklad detekcie dier v objekte pomocou HMT.

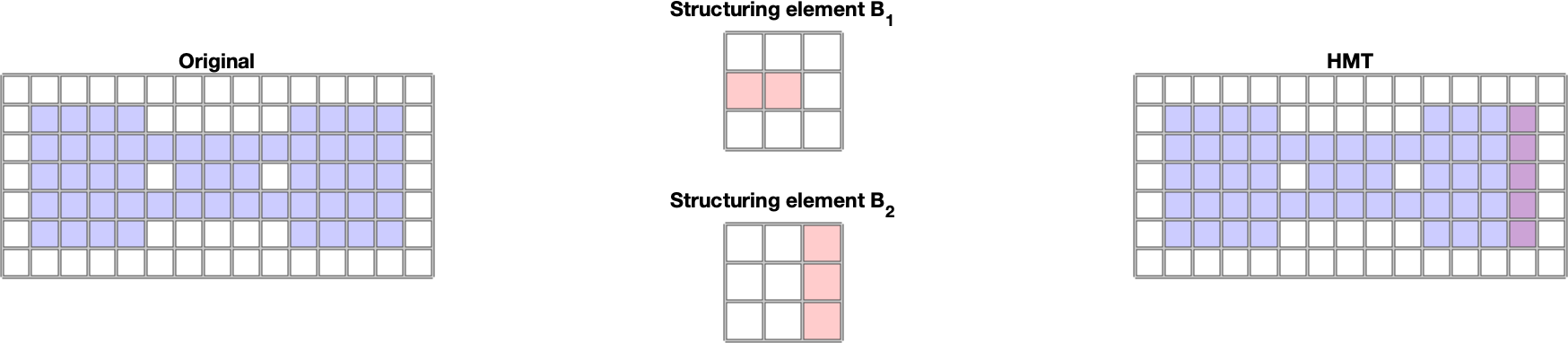
Obr. 4 Príklad detekcie pravej hrany objektu pomocou HMT.

Obr. 5 Príklad morfologickej rekonštrukcie časti objektu na základe počiatočného označenia.

Obr. 6 Príklad morfologickej rekonštrukcie využitej na vyplnenie objektu.

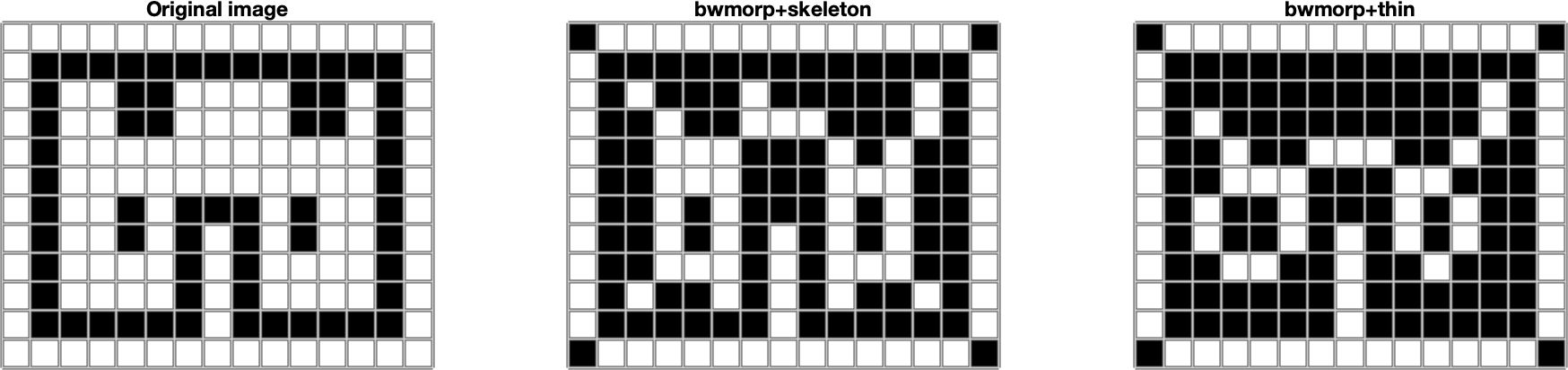
Obr. 7 Príklad tvorby kostry oblasti pomocou morfológie v prostredí MATLAB.

Viac informácii o morfologických operáciách je možné nájsť v [2] [3].

Referencie

[1] Mathworks, Morphological Operations, online: \url{https://www.mathworks.com/help/images/morphological-filtering.html}

[2] Gonzalez, R., C., Woods, E., W., Digital Image Processing, Global Edition, 4th edition, Pearson 2018, ISBN 10: 1-292-22304-9

[3] Gonzalez, R., C., Woods, E., W., Eddings, S., L., Digital Image Processing using MATLAB, Gatesmark Publishing, ISBN-10: 0-9820854-1-9

[4] Haralick, Robert M., and Linda G. Shapiro. Computer and Robot Vision, Volume I. Addison-Wesley, 1992.

Prílohy

Zdrojový kód programu, ktorý vytvoril Obr. 1

%https://en.wikipedia.org/wiki/Alpha_compositing
% RGBA images have 4 layers, the 4th is alpha channel:
% alpha value of 0 means that the pixel is fully transparent 
% alpha value of 1 means that the pixel is fully opaque.
clear all; close all; clc;
fig=figure;
%create some demo images
A=zeros(32,32);
A(6:21,6:21)=ones(16);
A(12:27,12:27)=ones(16);
A(12:15,12:15)=zeros(4);
SE=strel("diamond",4);
subplot(2,3,1)
showBlue(A, "Original");
subplot(2,3,4)
showRed(double(SE.Neighborhood), "Structuring element");
subplot(2,3,2)
B=imdilate(A,SE);
showCombined(A,B,"Dilation");
subplot(2,3,3)
B=imerode(A,SE);
showCombined(A,B,"Erosion");
subplot(2,3,5)
B=imopen(A,SE);
showCombined(A,B,"Opening");
subplot(2,3,6)
B=imclose(A,SE);
showCombined(A,B,"Closing");
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 10];
print(fig,"morphBinBasicsOps.png",'-dpng');

function showCombined(myA, myB,myTitle)
    %display A over B using transparency
    mySize=size(myA,1);
    zero=zeros(mySize);
    myImgaAlpha=0.2;
    myImgaRGBA=cat(3,zero,zero,myA,myImgaAlpha*myA);
    myImgbAlpha=0.2;
    myImgbRGBA=cat(3,myB,zero,zero,myImgbAlpha*myB);
    myC=myAoverB(myImgaRGBA, myImgbRGBA);
    imAshow(myC,myTitle);
end

function showBlue(myA,myTitle)
    mySize=size(myA,1);
    zero=zeros(mySize);
    myImgaAlpha=0.2;
    myImgaRGBA=cat(3,zero,zero,myA,myImgaAlpha*myA);
    imAshow(myImgaRGBA,myTitle);
end

function showRed(myA,myTitle)
    mySize=size(myA,1);
    zero=zeros(mySize);
    myImgaAlpha=0.2;
    myImgaRGBA=cat(3,myA,zero,zero,myImgaAlpha*myA);
    imAshow(myImgaRGBA,myTitle);
end

% display the RGBA image
% as background we use nontransparent white image
function imAshow(myRGBA, myTitle)
    mySize=size(myRGBA,1);
    one=ones(mySize);
    myWhite=cat(3,one,one,one,one);
    myOut=myAoverB(myRGBA,myWhite);
    if 0
        imshow(myOut(:,:,1:3));
    else
        %better traceable values
        myOut=uint8(myOut*255);
        imshow(myOut(:,:,1:3),[0,255],'InitialMagnification',"fit");
    end
    title(myTitle)
    pixelgrid 
end

%compute A over B for two RGBA images
function vOutImg=myAoverB(imgA, imgB)
    imgA_RGB=imgA(:,:,1:3);
    imgA_alpha=imgA(:,:,4);
    imgB_RGB=imgB(:,:,1:3);
    imgB_alpha=imgB(:,:,4);
    
    alpha_O=imgA_alpha+imgB_alpha.*(1-imgA_alpha);
    vOutImgRGB=(imgA_RGB.*imgA_alpha+imgB_RGB.*imgB_alpha.*(1-imgA_alpha))./alpha_O;
    vOutImgRGB(isnan(vOutImgRGB))=0;
    vOutImg=cat(3,vOutImgRGB,alpha_O);
end

Kľúčová časť programu, ktorý vytvoril Obr. 3

	...
	A= [...
	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
	0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
	0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
	0 1 1 1 1 0 1 1 1 0 1 1 1 1 0
	0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
	0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
	0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
	B1= [...
	1 1 1
	1 0 1
	1 1 1];
	B2= 1-B1;
	subplot(2,3,[1 4])
	showBlue(A, 'Original');
	subplot(2,3,2)
	showRed(B1, 'Structuring element B_1');
	subplot(2,3,5)
	showRed(B2, 'Structuring element B_2');
	subplot(2,3,[3 6])
	C=bwhitmiss(A,B1,B2)
	showCombined(A,C, 'HMT');
	...

Zdrojový kód programu, ktorý vytvoril Obr. 5

clear all; close all; clc;
fig=figure;
G= [...
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 1 1 1 0 0 0 0 0 1 1 1 1 0
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
F=zeros(size(G,1),size(G,2));
B= [...
     0 1 0
     1 1 1 
     0 1 0];
subplot(2,3,1)
showBW(G, 'Mask');
subplot(2,3,4)
showBW(B, 'Structuring element B');
subplot(2,3,2)
F1=F;F1(2,2)=1;
showBW(F1, 'Marker 1');
subplot(2,3,5)
F2=F;F2(8,2)=1;
showBW(F2, 'Marker 2');
subplot(2,3,3)
R1=imreconstruct(F1,G,B);
showBW(R1, 'Reconstruction 1');
subplot(2,3,6)
R2=imreconstruct(F2,G,B);
showBW(R2, 'Reconstruction 2');
fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,"morphBinRecon1.png",'-dpng');
function showBW(myImg, myTitle)

imshow(myImg,'InitialMagnification',"fit");
    title(myTitle)
    pixelgrid 
end

Zdrojový kód programu, ktorý vytvoril Obr. 6

clear all; close all; clc;
fig=figure;
G= [...
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 1 0 1 1 1 0 1 0 0 1 0
    0 1 0 0 1 0 1 0 1 0 1 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
F=zeros(size(G,1),size(G,2));
B= [...
     0 1 0
     1 1 1 
     0 1 0];
subplot(2,3,1)
showBW(G, 'Original image');
subplot(2,3,2)
showBW(B, 'Structuring element B');
subplot(2,3,3)
F(3,3)=1;
showBW(F, 'Marker');
subplot(2,3,4)
showBW(1-G, 'Mask = Original^C');
subplot(2,3,5)
R=imreconstruct(F,1-G,B);
showBW(R, 'Reconstruction');
subplot(2,3,6)
showBW(G+R, 'Filled = Original+reconstruction');

fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,"morphBinRecon2.png",'-dpng');
function showBW(myImg, myTitle)
    imshow(myImg,'InitialMagnification',"fit");
    title(myTitle)
    pixelgrid 
end

Zdrojový kód programu, ktorý vytvoril Obr. 7

clear all; close all; clc;
fig=figure;
A= [...
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
    0 1 1 1 1 1 1 1 1 1 1 1 1 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 1 1 0 0 0 0 1 1 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
    0 1 0 0 1 0 1 1 1 0 1 0 0 1 0
    0 1 0 0 1 0 1 0 1 0 1 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 0 0 0 0 1 0 1 0 0 0 0 1 0
    0 1 1 1 1 1 1 0 1 1 1 1 1 1 0 
    0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ];
subplot(1,3,1)
showBW(1-A, 'Original image');
subplot(1,3,2)
showBW(bwmorph(1-A,'skel',Inf),"bwmorp+skeleton");
subplot(1,3,3)
showBW(bwmorph(1-A,'thin',Inf),"bwmorp+thin");

fig.PaperUnits = 'inches';
fig.PaperPosition = [0 0 15 5];
print(fig,"morphBinSkel.png",'-dpng');
function showBW(myImg, myTitle)
    imshow(myImg,'InitialMagnification',"fit");
    title(myTitle)
    pixelgrid 
end

PDF verzia tejto stránky je dostupná tu: morphology_bw_sk.pdf